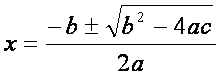Completing The Square
Completing The Square is a method for factoring and solving quadratic equations. In fact, by using the Completing The Square method, we can derive a general equation for solving quadratics, the familiar “Quadratic Formula”.
Let’s look at some examples first. We need to be able to recognize a perfect square when we see it. Let’s try (x+1)2. (x+1)2 = x2 + 2x + 1. If you are unfamiliar with the “FOIL” method, or how to multiply polynomials, make sure to visit the lesson on factoring before you continue with this section.
(x + 2)2 = x2 + 4x + 4, (x + 3)2 = x2 + 6x + 9, (x + 4)2 = x2 + 8x + 16, (x + 5)2 = x2 + 10x + 25
We notice a pattern here. The constant term is always one-half the middle term squared. Take a look at these examples until you see the pattern clearly. This gives us the basis for our completing the square method.
So, if we want to factor x2 + 6x + 9, we recognize the pattern and see that it is (x + 3)2. Polynomials that follow this pattern are known as “Perfect Squares”. But what if we want to factor a polynomial like x2 + 8x + 12? It is not a perfect square, so we need another way to solve this.
We use our pattern to create a perfect square: x2 + 8x + 12. Well, we know that in a perfect square, the constant term is one-half the middle term squared. In other words, ½ of 8 is 4, and 4 squared is 16. Thus, x2 + 8x + 16 is a perfect square.
Here is the trick: We want a 16 in our expression, but we don’t want to change the value of it. So we will add 16 and subtract it.
In other words: x2 + 8x + 12 = x2 + 8x + 12 ( + 16 - 16), and re-arrange it: x2 + 8x + 16 ( + 12 - 16). We re-group the expression, moving the 16 with the rest of the polynomial and moving the 12 to the end. So we now have: x2 + 8x +16 (- 4), and x2 + 8x + 16 is a perfect square which we can factor, so we now have:
x2 + 8x + 12 = (x + 4)2 – 4. Incidentally, this form of polynomial is called the “Vertex Form.”
The equation for the general quadratic is: ax2 + bx + c = f(x)
If we complete the square for this, we add/subtract 
to the expression. When we use some algebra to re-arrange this new expression, we get the familiar equation for solving quadratics:
