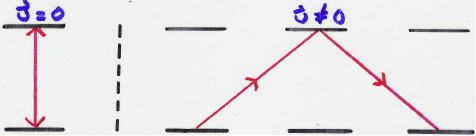


We will now prove this mathematically. For the moving frame of reference on the right, all the variables will have a prime mark over them (like t'). In the figure above, the vertical distance between the two mirrors is the same in both frames and is equal to h.
The total distance the light travels in the stationary frame is equal to 2h, or ct, since distance is rate times time. The speed of light is c, and the time it’s been moving for is t, so the total distance is ct.
To find the total distance in the moving frame of reference on the right, we will use the Pythagorean theorem, since the light beam carves out a triangle. The base of the triangle has a total length of ut' (d = ut). The path of the light is represented by the hypotenuses of the two triangles formed. We will use the Pythagorean theorem to find the length of those hypotenuses. The base of one of the triangles is ut'/2, and the height is 2h = ct. We can then find the length of the light’s path.